- Conduction Heat Transfer Equation
- Conduction Heat Transfer Schneider Steel
- Conduction Heat Transfer Schneider
- Conduction Heat Transfer Pdf
Lengston, “Heat Transfer from Multidimensional Objects Using One-Dimensional Solutions for Heat Loss,” Int. Heat Mass Transfer, 25, 149 (1982). CrossRef Google Scholar 8.

Conduction Heat Transfer Equation
Conduction Heat Transfer by Schneider, Paul J. At AbeBooks.co.uk - ISBN 10: - ISBN 13: 507 - Addison-Wesley Educational Publishers Inc - 1955 - Hardcover. This is Fourier's general conduction heat transfer equation for one-dimensional flow, (10) and all one-dimensional conduction problems: must satisfy this equation regardless of initial and boundary conditions. Schneider, Conduction Heat Transfer, 1st Ed., Mass., Addison-Wesley, 1955, p.
Conduction Heat Transfer Schneider Steel
It was an engineering laboratory report on heat conduction in metals and non-metals
source..Conduction Heat Transfer Schneider
Name
Course
Tutor’s Name
Institution
Date
Executive Summary
Thermal conducting or heat conduction is an important subject under the broad topic of heat transfer, and it mainly coves all phases of materials, that is, gases, liquids and solids. In more specific terms, thermal conductivity refers to the process through which collision and diffusion of microscopic particles or quasi-particles occur within a material, resulting in the transfer of internal energy due to thermal gradient. According to the P607 Climate and Energy Lecture 4(n.d) and the Physics classroom (2014), the internal energy is a combination of the microscopic potential and kinetic energy, which gets disorganized during the conduction process. Thermal conduction is also defined by parameters referred to as thermal coefficients, and these are usually determined experimentally through diverse laboratory tests. This report covers an investigation of three techniques of experimentally finding thermal coefficients of materials and summarize. The procedures followed in performing the experiment are highlighted, and the tests’ advantages and disadvantages given. A case study of a poor heat-conducting material that has been tested for its thermal conductivity values is also examined and the case study findings reviewed. The experimental computations or calculations are also presented in this report.
Introduction
Heat conduction is one of the heat transfer mechanisms which smooth temperature or thermal gradient (QPedia, n.d, Spring, 2008). The material heat transfer coefficients are vital parameters as far as heat transfer through conduction is concerned, since the characteristically define the conduction properties of a given material. Kurganov (2011) and Jakob (1958) say that the heat transfer coefficient has is a significant factor in addressing calculations and problems related to the external heat exchange between solid medium that conducts heat and its surroundings. It is a material characteristic that distinguishes between good heat conductors and poor heat conductors as well as determining different the different conductivities of conductive materials (Schneider, 1955). It is worth noting that there exist numerous means of determining the conduction coefficients, and this is the main concern of this experiment.
Theory for Experiment 1
The value of the thermal conductivity coefficient can also be obtained from the expression;
0001
where Q is the power, Ri is the inner radius l temperature, Ro is the outer radius, L is the length and Ti is the preceding temperature while To is the succeeding temperature recorded.
Theory for Experiment 2
The following are the parameters used in computing the heat transfer coefficient, each denoted by its respective letter: H is the total heat emitted, TA is the steady state temperature at disc A, TB is the steady state temperature at disc B, TC is the steady state temperature at disc C, V=potential difference across the element, I=the amperage of current, hs is the heat energy flowing through the specimen K is the thermal conductivity coefficient, t is the thickness, r is the radius of the disc, while aA, aB, aC, aS, are the exposed surface areas of discs A, B , C, and S. The energy e, emitted from each exposed unit area in Joules, is related to the total heat emitted H as shown in the following relation:
0001
This equation is derived from the mathematical integration of the energy equation as shown by Knudsen, Hottel, Sarofim, Wankat and Knaebel (1997) and Venkanna (2010), who also show mathematically that the heat-transfer coefficient is a function of temperature gradients.
The heat supplied to the heating element is the given by 0013 QUOTE 0001 001400010015 , the product of the potential difference and the amperage is equivalent to the power supplied to the heater (Adiutory, 1974 and Alifanov, Artioukhine and Rumyantsev, 1995). Therefore, it is seen that from the two expressions, the following equation of energy is obtained:
0001
Rearranging this equation to make K the subject of the expression yields the following equation:
0001
Assumptions
The heat transfer between an object and its surroundings depends on the exposed area of the object and the temperature difference between the two for all the specimen discs.
The conditions of equilibrium are met and the temperature of the specimen S is the mean temperature of the discs A and B.
Procedure for Experiment 1
The spacing between the output probes, the disc and the thickness was measured and recorded. The output probes leads were then attached to the numbered probes, and it was ensured that the water was flowing on the heater to a low power of about 5 watts. All the temperatures were recorded once T1 was fairly stable. The power was increased to 15 watts, and the recordings repeated, and this was done for 20 watts too, after giving time for stabilization. The power was then turned off, and water allowed to flow for 5 minutes before being turned off.
Procedure for Experiment 1
The sample material to be tested was prepared in the form of a thin disc of the same diameter as the copper discs that constituted the apparatus. It was ensured that the disc was flat and smooth for good thermal contact to be achieved before the thicknesses and the diameters of the discs labeled A, B, C and the specimen S were measured. The discs and the heater were wiped clean of dust, and placed in the frame in the following order: disc A, specimen S, disc B, heater disc C. Before the clamp screw was tightened to firmly hold the discs, it was certified that all the thermometer holes were pointing in the upward direction, and then, a small quantity of glycerin was placed in each thermometer hole, followed by the thermometer. The heater terminals were then connected to a 6V power supply via a rheostat and an ampere, while a voltmeter was connected across the heater terminals. For the purposes of measuring the ambient temperature, a fourth thermometer was placed fairly close to the apparatus, followed by the connection of the electrical circuit, where the current was allowed to flow through the heater, and the apparatus left to achieve equilibrium: all the readings were then taken and recorded.
Other Methods of Experimentally Finding Thermal Coefficients
The Two-Phase Thermosyphons Method
This is one of the methods used in obtaining heat conduction coefficients, and it entails measuring the temperature variation for small material blocks with time. According to Milanez and Mantelli (2004), aluminum blocks are polished, painted black and then tested for temperature and heat transfer coefficients in an enclosure system. The temperature distribution test entails obtaining the temperature of different points of the enclosure control volume dimensionally designed in parallelepiped form using thermocouples. On the other hand, the measurement of the heat transfer coefficients entails measuring the heat flux distribution inside the cavity of the enclosure using the metallic blocks. Mathematical expressions that relate the mass of the blocks and their specific heat capacities are then applied to compute the coefficients of heat transfer.
Procedure for the Two-Phase Thermosyphons Method
Some sheets of mild steel with the desired experimental dimensions, preferably 0.38m x 0.48m x 0.61m, are arranged into a rectangular enclosure. This is followed by attaching four pairs of thermosyphons to the inner side of the enclosure side walls so that these side walls serve as fins that assist in dissipating the heat from the thermosyphon condensers. The evaporators of the thermosyphon are situated inside a combustion chamber and tilted at 45° below the enclosure. At the back and the front of the enclosure, two metal sheets are riveted, and the enclosure walls and thermosyphons are wrapped with an insulating blanket of glass wool, with some mild steel sheets that are placed on the external side being used for the purpose of protecting this blanket. The enclosure is completed by a front door that comprises of metal sheets which sandwiches glass wool, with an inspection glass window being located at the center of the front door. With this setup, the transient and steady state temperatures are measured by the thermocouples and then applied to compute the heat conduction coefficients.
Advantages and Disadvantages
The advantages of this method include low thermal resistance and uniformity in temperature distribution. The disadvantages constitute concentrating more on the radiation and convective coefficients than on conductivity coefficients.
Inverse Heat Conduction Iterative Technique
The other method is the inverse heat conduction iterative technique commonly used in quenching process, where an iterative regularization algorithm is used to solve the problem (Felde, Réti, Sarmiento, Smoljan and Deus, n.d). This method relies on the parameters that govern temperature distribution patterns with regard to a homogeneous isotropic domain that constitutes constant material characteristics. The heat transfer coefficient is then predicted iteratively as a function of surface temperature using software called SQintegra. The data needed for this method include temperature-time>
Conduction Heat Transfer Pdf
Download our conduction heat transfer schneider eBooks for free and learn more about conduction heat transfer schneider . These books contain exercises and tutorials to improve your practical skills, at all levels!
You can download PDF versions of the user's guide, manuals and ebooks about conduction heat transfer schneider, you can also find and download for free A free online manual (notices) with beginner and intermediate, Downloads Documentation, You can download PDF files about conduction heat transfer schneider for free, but please respect copyrighted ebooks.
To find more books about conduction heat transfer schneider
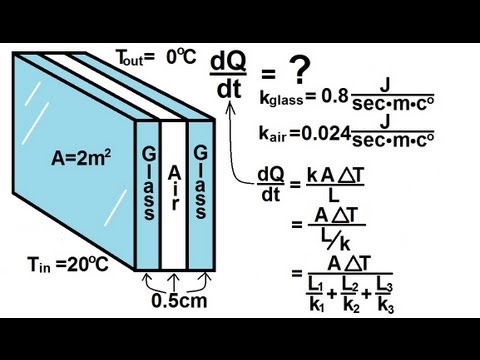 , you can use related keywords :
, you can use related keywords :Similar Books to conduction heat transfer schneider
All books are the property of their respective owners.
pdf-book-search.com does not host pdf files, does not store any files on its server, all document are the property of their respective owners. This site is a Google powered search engine that queries Google to show PDF search results.
pdf-book-search.com is a custom search engine powered by Google for searching pdf files. All search results are from google search results. Please respect the publisher and the author for their creations if their books are copyrighted. Please contact us or the content providers to delete copyright contents if any and email us, we'll remove relevant links or contents immediately. Be sure to respect the publishers and the authors office file copyright. Submit us a DMCA notice and Inform about office files copyright abuse, using contact form .